오늘은 전기 이론의 집대성인 옴의 법칙에 대해 알아보겠습니다.
모든 전기는 옴의 법칙에서 시작된다고 해도 과언이 아닙니다.
우리는 이 포스트에서 확실히 배울 것입니다.
옴의 법칙 공식
$V=IR$
이 개념은 “물”에 비유하면 쉽게 이해할 수 있습니다.
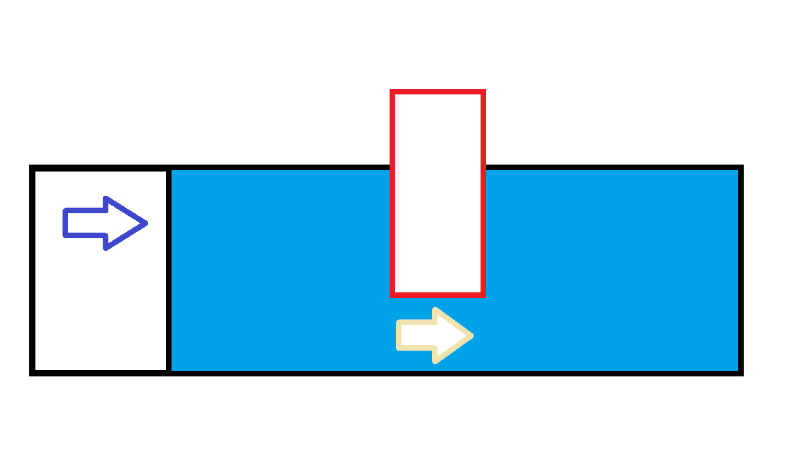
V는 전기압 ‘수압’
나는 “물”
저항인 벽과 같은 “장애물”로 R을 표현합시다.
마치 주사와 같습니다.
수압은 물이 장애물을 넘을 수 있도록 하는 에너지를 제공합니다.
물은 장애물을 넘어야 하는 대상이다.
장애물은 물이 원활하게 흐르지 못하게 막는 벽입니다.
* 장애물이 클수록 같은 양의 물을 얻기 위해 더 높은 수압이 필요합니다.
I가 일정할 때 R과 V는 비례합니다.
빨간 장애물이 커져도 파란 추진력이 강하기 때문에 수평을 맞춰줍니다.
전류는 같은 양이 흐를 때의 이미지입니다.
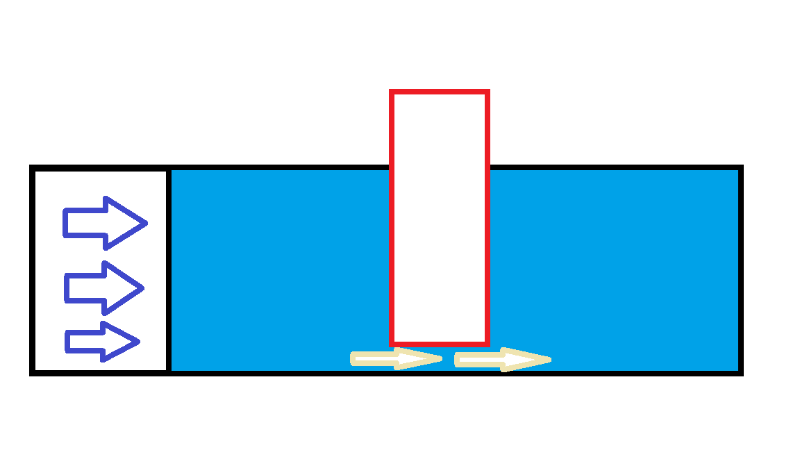
* 장애물이 일정하면 수압이 높아질수록 흐르는 물의 양도 자연히 많아집니다.
R이 일정할 때 V와 I는 비례합니다.
파란색의 인쇄력이 높아질수록 노란색 패스의 양도 증가합니다.
주사기를 짜면 압력이 높아지고 공기가 한 곳에 모입니다.
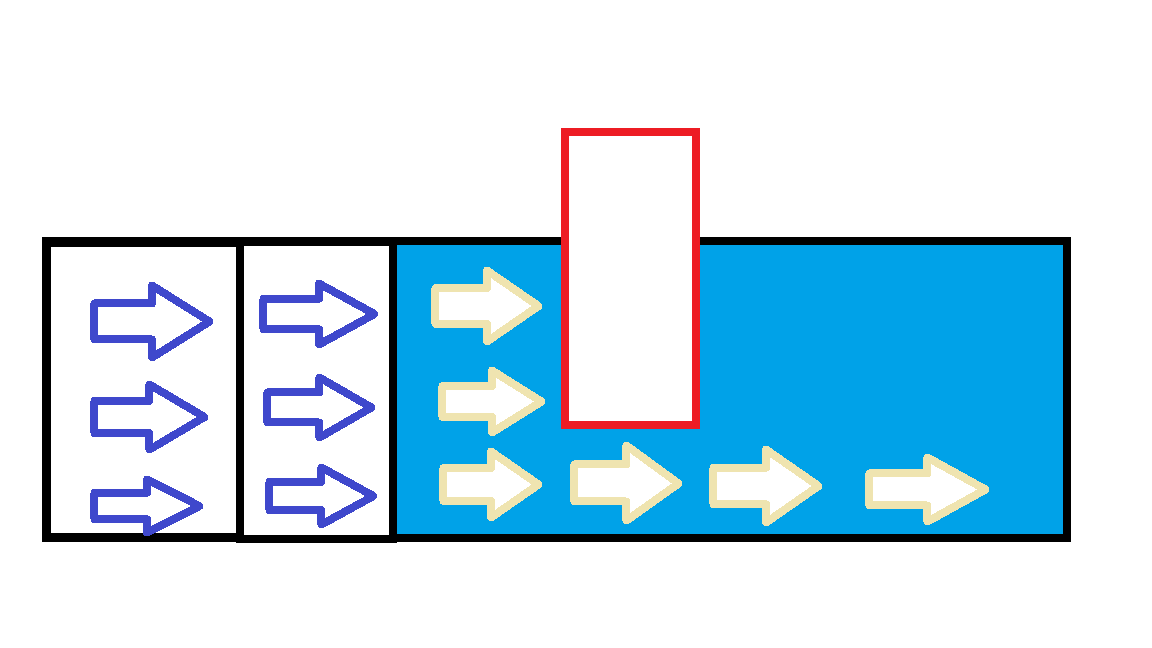
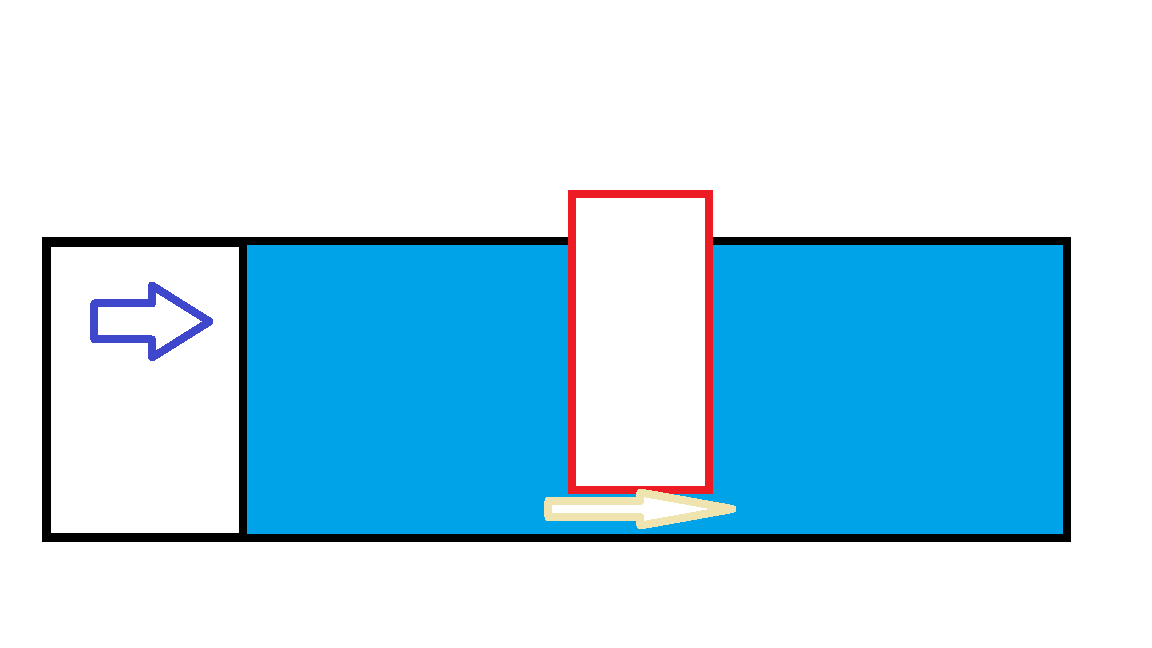
*수압이 일정하면 장애물이 클수록 물이 덜 흐를 수 있습니다.
V가 일정할 때 I와 R은 반비례합니다.
파란색 압력이 일정하면 자연스럽게 흐를 수 있는 노란색은 장애물이 커질수록 줄어듭니다.
도로가 사라져 고속도로에 갇힌 자동차와 같습니다.
계산은 수식에 직접 삽입하여 수행됩니다. 옴의 법칙은 단순하기 때문에 배우기 쉽습니다.
이 법은 기본보다 실제로 더 중요합니다. 대부분의 게시물에서 사용할 것입니다.
예를 들어 보겠습니다.
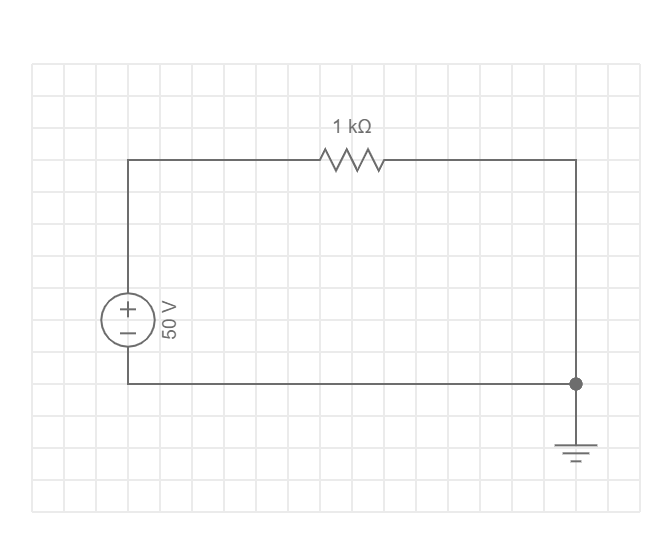
이 회로에 흐르는 전류 I는?
솔루션: I = V/R
I=50(V)/1000(Ω)=0.05(A)=50(mA)
답변: 50(mA)
작업을 풀 때 m(밀리) 및 k(킬로)와 같은 단위에 주의하십시오.
추가 응용 개념(전하 및 전자)
우리는 전기가 전자의 흐름이라는 것을 배웠습니다.
얼마나 많은 전자가 흐르나요? 다음 공식을 살펴보자
$I=Q/t$
Q 요금의 개념
이 시점에서 Q는 요금입니다. 즉, 전기량을 나타내는 기호입니다. 단위는 1(C)(쿨롱)입니다.
때가됐다. 1 초. 즉, 1초 동안 1(C)까지 흐르는 전류의 양을 1A라고 한다.
이때 양성자는 + 기호를, 전자는 – 기호를 추가하여 표현한다.
*따라서 전류와 전자의 방향이 반대이다.
전자가 발견되기 전에는 전류를 정의할 때 +에서 -로 흐르는 것으로 해석되었습니다.
하지만 그 후 움직이는 것은 음의 극성 전자입니다.나는 그것을 나중에 알았다.
기존 과학을 처음부터 바꾸는 것은 너무 큰 일이었습니다.
그래서 전류의 방향을 현재(+에서 -)로 해석하기로 했습니다.
일반적인 회로 분석에서는 전류를 중심으로 분석하면 충분하다.
물리적 시간에서 전자의 운동을 계산할 때 ‘-‘를 추가하면 방향이 바뀌므로 상관이 없습니다.
전자의 전하는 무엇입니까?
1(C)는 1초에 6.25*10^18개의 전자에 흐르는 전류의 양이다.
전자공학에서 전자의 전하는 1e로 표현된다. (전자의 약자)
전자의 질량은 9.109 * 10^-31(kg)입니다.
전자 1e(C)는 어떤 전하를 가지고 있습니까? 유도하는 방법을 알아 봅시다.
유도 방식
1 (C} : 6.25*10^18 전자 = 1 전자의 전하 (C) : 1 전자
왼쪽 비례식에 양쪽을 똑같이 나누는 원리를 대입하여 전자의 수를 6.25*10^18로 나누자.
1/6.25*10^18 (C) : 1 전자 = 1 전자의 전하 (C) : 1 전자
전자의 전하(C) = 1/6.25*10^18(C)
전자의 전하(C) = 1.602*10^-19(C).
여기서 기호 ‘-‘는 전자의 전하가 음수이기 때문에 추가됩니다.
다시 말해서 1e = -1.602*10^-19(C).
정리하다
1(C)의 전자 수 6.25*10^18(개)
수수료 1e 1e = -1.602*10^-19 (C)
1e의 무게는 9.109*10^-31(kg)입니다.
맺음말
오늘은 옴의 법칙과 전하, 전자에 대한 설명을 살펴보았습니다.
옴의 법칙은 회로를 공부할 때 가장 먼저 필요한 공식입니다.
다만 원리가 단순하기 때문에 응용 개념을 추가로 만들었다.
회로를 해석할 때 옴의 법칙만 이해하면 됩니다.
오늘 수고하셨습니다. 다음 포스트에서 만나요.
*어떻게든 잘 그리려고 노력했습니다.
부대에서 올릴 시간이 없어서 아직 엉성한(?)게 남아있습니다.
화살의 크기가 불편하신 분들을 향한 인간애를 부탁드립니다.

